Question 1.
Construct the following angles at the initial point of a given ray and justify the construction.
a) 90°
Solution:
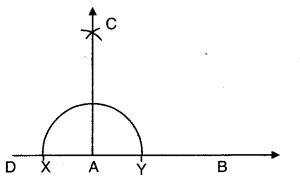
- Let AB be the given ray.
- Produce BA to D.
- Taking A as centre draw a semi circle with some radius.
- With X and Y as Center draw two intersecting arcs of same radius.
Or
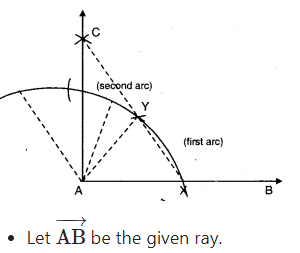
- With A as centre draw an arc of any radius.
- Mark off two equal arcs from X as shown in the figure with the same radius taken as before.
- Bisect the second segment.
- Join the point of intersection of above arcs, with A.
- ∠BAC is the required right angle.
- Join the point of intersection ‘C’ and ‘A’.
- ∠BAC = 90°
In ΔAXY; ∠YAX = 60° and
in ΔAYC ∠YAC = 30° ∠BAC = 90°
b) 45°
Solution:
Steps:
- Construct 90° with the given ray AB.
- Bisect it from ∠BAD = 45°
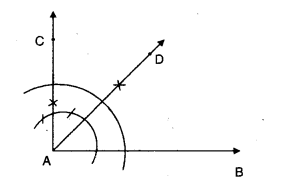
or
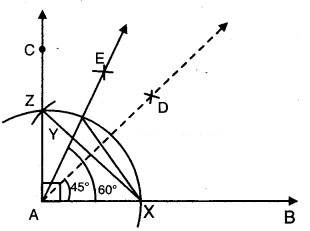
Steps:
- Construct ∠BAC = 60°
- Bisect ∠BAC = ∠DAC = 30°
- Bisect ∠DAC such that ∠DAE = ∠FAC = 15°
- ∠BAE=45°
ΔAXZ is equilateral
and ∠YAZ = 15°
∴∠XAY = 45°
Question 2.
Construct the following angles using ruler and compass and verify by measuring them by a protractor.
a) 30°
Solution:
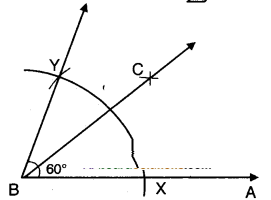
- Construct ∠ABY = 60°
- Bisect ∠ABY = 60°
- Such that ∠ABC = ∠CBY = 30°
b) 22 1°/2
Solution:
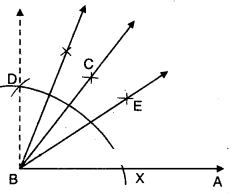
- Construct ∠ABD = 90°.
- Bisect ∠ABD such that ∠ABC = ∠CBD = 45°
- Bisect ∠ABC such that
∠ABE = ∠EBC = 22 1°/2
c) 15°
Solution:
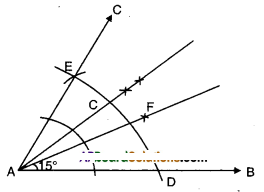
Steps of construction : ,
- Construct ∠BAE = 60°
- Bisect ∠BAE such that ∠BAC = ∠CAE = 30°
- Bisect ∠BAC such that ∠BAF = ∠FAC = 15°
d) 75°
Solution:
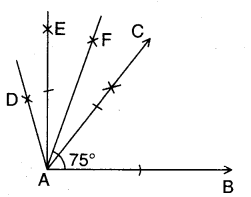
Steps of construction :
- Construct ∠BAC = 60°
- Construct ∠CAD = 60°
- Bisect ∠CAD such that ∠BAE = 90°
- Bisect ∠CAE such that ∠BAF = 75°
e) 105°
Solution:
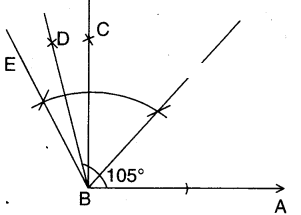
Steps of construction:
- Construct ∠ABC = 90°
- Construct ∠CBE = 30°
- Bisect ∠CBE such that the angle formed ∠ABD = 105°
f) 135°
Solution:
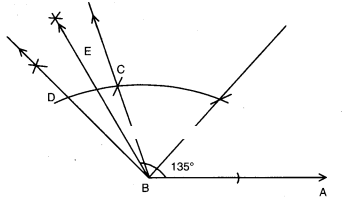
Steps of construction:
- Construct ∠ABC = 120°
- Construct ∠CBD = 30°
- Bisect ∠CBD such that the angle formed ∠ABE = 135°
Question 3.
Construct an equilateral triangle, given its side of length of 4.5 cm and justify the constraction.
Solution:A.
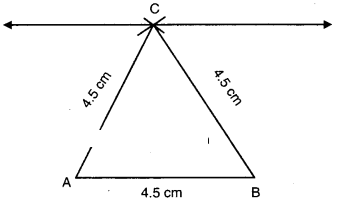
- Draw a line segment AB = 4.5 cm.
- With B and A as centres draw two arcs of radius 4.5 cm meeting at C.
- Join C to A and B.
- ΔABC is the required triangle.
Justification:
In ΔABC
AB = ∠C ⇒ ∠C = ∠B
Also AB = BC ⇒ ∠C = ∠A
Hence ∠A = ∠B = ∠C
But ∠A + ∠B + ∠C = 180°
∴ ∠A = ∠B = ∠C = 180°/3 = 60°
Question 4.
Construct an isosceles triangle, given its base and base angle and justify the construction. [Hint: You can take any measure of side and angle]
Solution:
A.
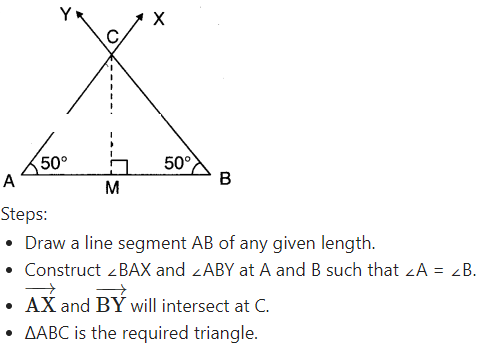
Justification:
Drop a perpendicular CM to AB from C.
Now in ΔAMC and ΔBMC
∠AMC = ∠BMC [Right angle]
∠A = ∠B [Construction]
CM = CM (Common)
∴ ΔAMC ≅ ΔBMC
⇒ AC = BC [CPCT]
Question 1.
Construct AABC in which BC = 7 cm,∠B = 75° and AB + AC =12 cm.
Solution:
A.
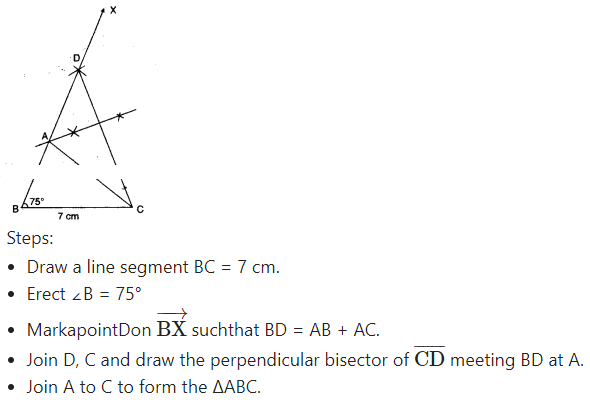
Question 2.
Construct ΔPQR in which QR = 8 cm, ∠B = 60° and AB - AC = 3.5 cm.
Read ∠Q = 60°and PQ - PR = 3.5 cm
Solution:
A.
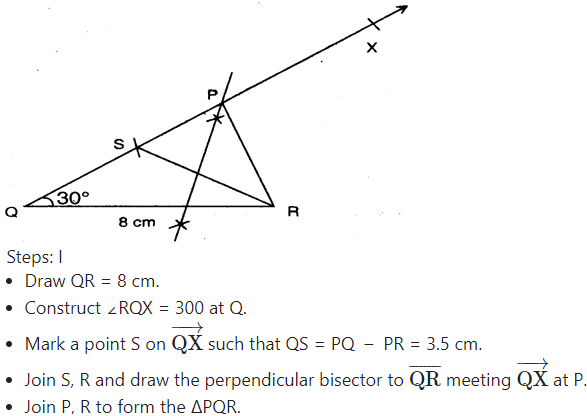
Question 3.
Construct ΔXYZ in which ∠Y = 30 °; ∠Z = 60 ° and XY + YZ + ZX = 10 cm.
Solution:
A.
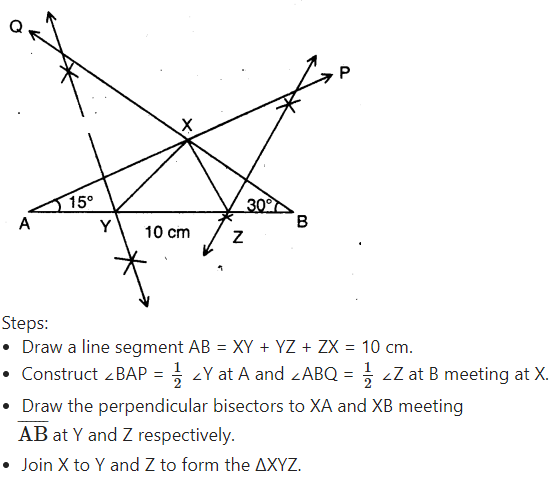
Question 4.
Construct a right triangle whose base is 7.5 cm and sum of its hypotenuse and otherside is 15 cm.
Solution:
A.
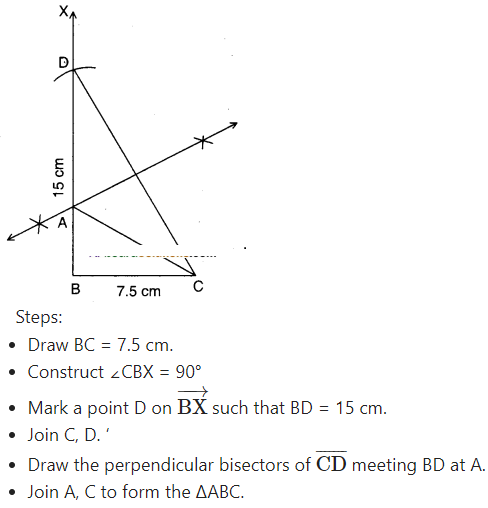
Question 5.
Construct a segment of a circle on a chord of length 5 cm containing the following angles i) 90° ii) 45° iii) 120°
Solution:
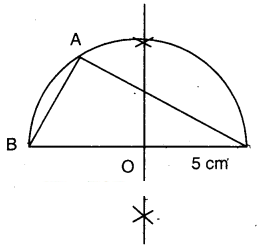
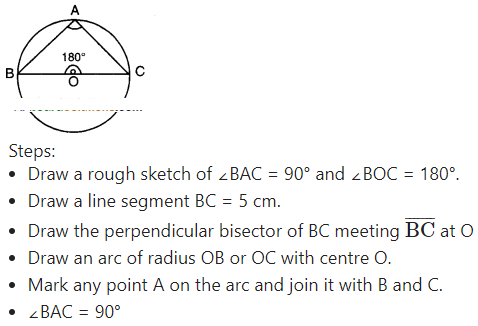
i) 90°
A.
ii) 45°
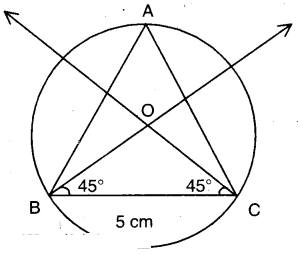
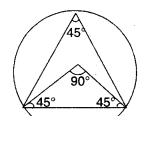
Steps:
- Draw a line segment BC = 5 cm.
- Construct ABOC such that BC = 5 cm, ∠B = 45° = ∠C.
- Draw a circle segment of radius OB or OC with centre ’O’.
- Mark any point A on the segment and join it with B and C.
- ∠BAC = 45°
iii) 120°
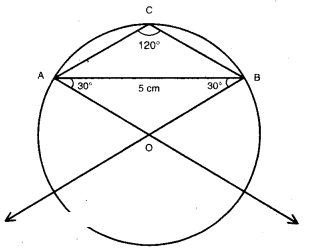
Steps:
- Draw a line segment AB = 5 cm. ,
- Construct ΔAOB in which ∠A = 30°; ∠B = 30°; AB = 5 cm.
- With ‘O’ as centre draw a circle segment.
- On the opposite side make any point C and join it with B and C.
- ∠ACB = 120°